Atan2

Defined in header <cmath>.

Description

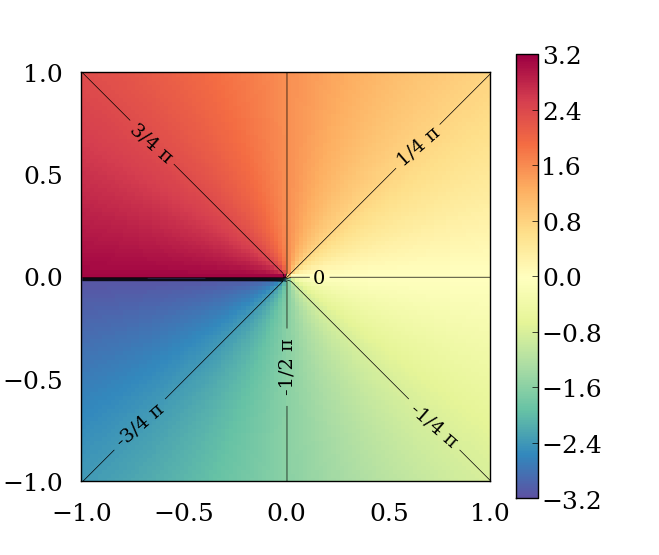
Computes the arc tangent of y / x using the signs of arguments to determine the correct quadrant.
The library provides overloads of std::atan2 for all cv-unqualified floating-point types as the type of the parameters y and x  (since C++23).
Additional Overloads are provided for all other combinations of arithmetic types  (since C++11).

Declarations

C++23

// 1)
/* floating-point-type */ atan2( /* floating-point-type */ y,
                                 /* floating-point-type */ x );
// 2)
float atan2f( float y, float x );
// 3)
long double atan2l( long double y, long double x );

Additional Overloads

// 4)
template< class Arithmetic1, class Arithmetic2 >
/* common-floating-point-type */ atan2( Arithmetic1 y, Arithmetic2 x );

C++11

// 1)
float atan2 ( float y, float x );
// 2)
double atan2 ( double y, double x );
// 3)
long double atan2 ( long double y, long double x );
// 4)
float atan2f( float y, float x );
// 5)
long double atan2l( long double y, long double x );

Additional Overloads

// 6)
template< class Arithmetic1, class Arithmetic2 >
/* common-floating-point-type */ atan2( Arithmetic1 y, Arithmetic2 x );

Parameters

y, x - floating-point or integer values

Return value

If no errors occur, the arc tangent of y / x (arctan(x/y)) in the range [-π, +π] radians, is returned.

If a domain error occurs, an implementation-defined value is returned (NaN where supported).

If a range error occurs due to underflow, the correct result (after rounding) is returned.

Error handling

Errors are reported as specified in math_errhandling.

Domain error may occur if x and y are both zero.

If the implementation supports IEEE floating-point arithmetic (IEC 60559),

• If x and y are both zero, domain error does not occur
• If x and y are both zero, range error does not occur either
• If y is zero, pole error does not occur
• If y is ±0 and x is negative or -0, ±π is returned
• If y is ±0 and x is positive or +0, ±0 is returned
• If y is ±∞ and x is finite, ±π/2 is returned
• If y is ±∞ and x is -∞, ±3π/4 is returned
• If y is ±∞ and x is +∞, ±π/4 is returned
• If x is ±0 and y is negative, -π/2 is returned
• If x is ±0 and y is positive, +π/2 is returned
• If x is -∞ and y is finite and positive, +π is returned
• If x is -∞ and y is finite and negative, -π is returned
• If x is +∞ and y is finite and positive, +0 is returned
• If x is +∞ and y is finite and negative, -0 is returned
• If either x is NaN or y is NaN, NaN is returned

Notes

std::atan2(y, x) is equivalent to

std::arg(std::complex<std::common_type_t<decltype(x), decltype(y)>>(x, y))

POSIX specifies that in case of underflow, y / x is the value returned, and if that is not supported, an implementation-defined value no greater than DBL_MIN, FLT_MIN, and LDBL_MIN is returned.

The additional overloads are not required to be provided exactly as Additional Overloads. They only need to be sufficient to ensure that for their first argument num1 and second argument num2:

If num1 or num2 has type long double, then
std::atan2(num1, num2) has the same effect as
​std::atan2(static_cast<long double>(num1), static_cast<long double>(num2)).

Otherwise, if num1 and/or num2 has type double or an integer type, then
std::atan2(num1, num2) has the same effect as
​std::atan2(static_cast<double>(num1), static_cast<double>(num2)).

Otherwise, if num1 or num2 has type float, then
std::atan2(num1, num2) has the same effect as
​std::atan2(static_cast<float>(num1), static_cast<float>(num2)). (until C++23)

If num1 and num2 have arithmetic types, then
std::atan2(num1, num2) has the same effect as
std::atan2(static_cast</* common-floating-point-type */>(num1), static_cast</* common-floating-point-type */>(num2)).

where /* common-floating-point-type */ is the floating-point type with the greatest floating-point conversion rank and greatest floating-point conversion subrank between the types of num1 and num2, arguments of integer type are considered to have the same floating-point conversion rank as double.

If no such floating-point type with the greatest rank and subrank exists, then overload resolution does not result in a usable candidate from the overloads provided.

Examples

#include <cmath>
#include <iostream>
 
void print_coordinates(int x, int y)
{
    std::cout 
        << std::showpos
        << "(x:" << x << ", y:" 
        << y << ") cartesian is "
        << "(r:" << std::hypot(x, y)
        << ", phi:" << std::atan2(y, x) 
        << ") polar\n";
}
 
int main()
{
    // normal usage: the signs of the two arguments determine the quadrant
    print_coordinates(+1, +1); 
    // atan2( 1,  1) =  +pi/4, Quad I
    print_coordinates(-1, +1); 
    // atan2( 1, -1) = +3pi/4, Quad II
    print_coordinates(-1, -1); 
    // atan2(-1, -1) = -3pi/4, Quad III
    print_coordinates(+1, -1); 
    // atan2(-1,  1) =  -pi/4, Quad IV
 
    // special values
    std::cout 
        << std::noshowpos
        << "atan2(0, 0) = " 
        << atan2(0, 0) << '\n'
        << "atan2(0,-0) = " 
        << atan2(0, -0.0) << '\n'
        << "atan2(7, 0) = " 
        << atan2(7, 0) << '\n'
        << "atan2(7,-0) = " 
        << atan2(7, -0.0) << '\n';
}

Result

(x:+1, y:+1) cartesian is (r:1.41421, phi:0.785398) polar
(x:-1, y:+1) cartesian is (r:1.41421, phi:2.35619) polar
(x:-1, y:-1) cartesian is (r:1.41421, phi:-2.35619) polar
(x:+1, y:-1) cartesian is (r:1.41421, phi:-0.785398) polar
atan2(0, 0) = 0
atan2(0,-0) = 3.14159
atan2(7, 0) = 1.5708
atan2(7,-0) = 1.5708